Scaling Behaviour and Critical Phase Transitions in Integrated Information Theory

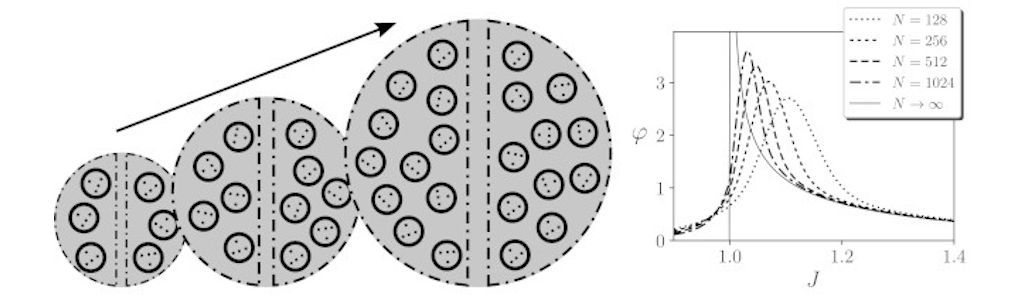
I just published a new paper exploring some of the ideas we initiated in our Integrated information in the thermodynamic limit (Aguilera & Di Paolo, 2019) paper. Here, I explore in detail many of the assumptions of Integrated Information Theory (specifically IIT 3.0) by computing integration in large kinetic Ising networks presenting a critical point. By combining a simple model with tractable statistical properties that can be analytically characterized with architectures, I show that some assumptions in the theory are problematic for capturing some of the properties associated with critical phase transitions. This example compels researchers interested in IIT and related indices of complexity to apply such measures under careful examination of their design assumptions. Rather than applying the measure off-the-shelf, this work offers some methods to explore in more depth the assumptions behind the measure and how they apply to each situation

Aguilera, M (2019). Scaling Behaviour and Critical Phase Transitions in Integrated Information Theory. Entropy 2019, 21(12), 1198; https://doi.org/10.3390/e21121198

Abstract

Integrated Information Theory proposes a measure of conscious activity ($\Phi$), characterised as the irreducibility of a dynamical system to the sum of its components. Due to its computational cost, current versions of the theory (IIT 3.0) are difficult to apply to systems larger than a dozen units, and, in general, it is not well known how integrated information scales as systems grow larger in size. In this article, we propose to study the scaling behaviour of integrated information in a simple model of a critical phase transition: an infinite-range kinetic Ising model. In this model, we assume a homogeneous distribution of couplings to simplify the computation of integrated information. This simplified model allows us to critically review some of the design assumptions behind the measure and connect its properties with well-known phenomena in phase transitions in statistical mechanics. As a result, we point to some aspects of the mathematical definitions of IIT 3.0 that fail to capture critical phase transitions and propose a reformulation of the assumptions made by integrated information measures.

Written on December 17th, 2019 by Miguel Aguilera